Компьютерная графика
Кодовое дерево Хаффмена
Рисунок 98. Кодовое дерево Хаффмена
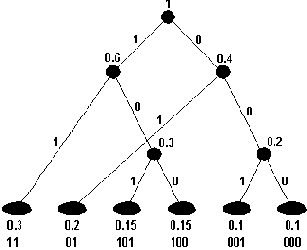
Средняя длина кодового слова вычисляется как взвешенная вероятностями сумма длин всех кодовых слов:
Lcp = p1L1 + p2L2 + ... + pnLn,
где p1,..., pn — вероятности кодовых слов;
L1,..., Ln — длины кодовых слов.
Клод Шеннон в 40-х годах XX века в своей «Математической теории связи»
показал, что средняя длина кодового слова не может быть меньше, чем энтропия множества кодируемых элементов, которая вычисляется по формуле:
Н = p1log(1/p1) + p2log(l/p2) + ... + pnlog(l/ pn)
Средняя длина кодового слова, обеспечиваемая кодом Хаффмена, приближается к энтропии при очень больших объемах сообщений. При этом длина кодового слова, имеющего вероятность р, приближается к log (l/p). В случае кодирования двоичными символами основание логарифмов в приведенных выше формулах равно 2.
Если не учитывать вероятности (т. е. считать их равными), то для кодирования n элементов с помощью нулей и единиц потребуется log(n) битов на каждый элемент. Точнее говоря, в качестве длины слова следует взять ближайшее большее целое для этого числа. Так, например, для кодирования 6 элементов потребуются слова длиной 3 (log(6) = 2,585). При этом все слова будут иметь одинаковую длину. Если же учесть вероятности, то для рассмотренного выше примера средняя длина кодового слова будет равна 2,5 (0,5x2 + 0,5x3). При кодировании достаточно больших сообщений это дает экономию около 17%.
Код Хаффмена реализует обратимое и максимальное сжатие данных (обратимость означает, что имеется возможность полного восстановления исходного сообщения). Максимальность сжатия понимается в следующем смысле. Если источник сообщений генерирует символы с фиксированным распределением вероятностей, то при кодировании сообщений, длина которых стремится к бесконечности, достигается средняя длина кодового слова, равная энтропии. Следует заметить, что для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Хаффмена, но все они дают одинаковые результаты.
Существует еще один алгоритм сжатия — Шеннона-Фано, основанный на тех же идеях, но не гарантирующий максимального сжатия, как алгоритм Хаффмена. Код Шеннона-Фано строится с помощью дерева. Однако построение этого дерева начинается от корня. Все множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмена.
